最新の5件
[凍結破損関連]
[凍結破損関連]
[凍結破損関連]
[凍結破損関連]
[凍結破損関連]
System time 0.031250
マスターの独り言
| 凍結破損のメカニズム3 (凍結破損裁判その4) >> |
- 凍結破損のメカニズム4 (凍結破損裁判その5)
-
【2015/03/04(水)】
[凍結破損関連]
<<凍結破損裁判(その4)>> の続き
前回は水道管(鋼管)が凍結により破裂する現象について述べました。今回はステンレス製フレキシブル管の凍結による破損についてと、応力の集中、一般的に水道管が凍結破損に至る状況等について記述します。
※以下の文章はK技研の行った実験に対する反論として、私が記述し裁判所に提出した(はずの)書類を元にしています。今回Webに公開するにあたり、K技研の実験結果を公表しても良いのか不明であることから、その情報不足を補うため加筆訂正を行い、また言い回しやレイアウトの変更もしています。
※研究者でも無い者が記述した文章であるため、計算ミスや事実と異なる記述があるかも知れません。文責は私にありますが、もしお気づきの点がありましたら、お知らせいただければ幸いです。
凍結破損のメカニズムについて(4)
【フレキ管の降伏圧について】
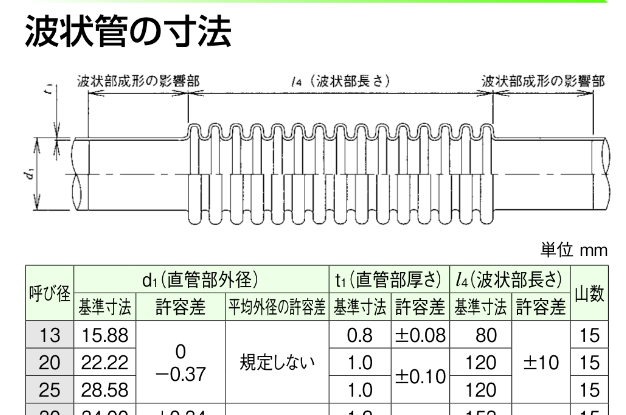
ステンレスフレキシブル管(以下、フレキ管)については、一般に使用されている物の物性表が見当たらなかったため、より信頼性があると思われる水道用波状ステンレス鋼管(13Su)のデータ※6を次に示します。
引張り強さ:520N/mm2外径:15.88mm内径:14.28mmであるから、これを元に降伏圧を計算すると次のようになります。2×(520 / 2)×ln(15.88 / 14.28) ≒ 55.22(MPa)図を見てもらえれば分かるように、ここでは蛇腹部分ではなく直管部分の外径を用い、また、せん断強度を下降伏点ではなく、より値いの高い引張り強さを元にして計算しています。蛇腹部分の外径は直管部分よりも大きくなりますので、降伏圧はこれより低くなります。
つまり、上記の値いは十分な余裕を持たせたものであるわけですが、それでも降伏圧の55.22MPaというのは温度にしてわずか−4.79℃になります。
蛇腹管(フレキ管)は鋼管に比べ膨張変形の許容度が遥かに高く、氷の体積膨張率から考えて、例え−22℃まで冷却しても一度の凍結で破損する可能性は低いと言えますが、新品の値いですらこれですから、管内凍結を繰り返し、膨張変形が限度に達すると−4℃程度の温度でも簡単に破損することが分かります。
氷の圧力と温度の計算に関して
氷の圧力と温度はほぼ比例の関係にあり、圧力と温度をプロットしたグラフは直線に近い穏やかな曲線を描きます(図-2の縦軸は対数表記であることに注意)
この曲線は融解曲線ともいうのですが、圧力と温度の関係を表す近似式については適切な記述を見つけることが出来ませんでした。
そこで、融解曲線が2次曲線の一部に類似していることから、0.1MPa/0℃、210MPa/-22℃、-5℃における圧力を57.57MPaとして次の式を導いたところ、近似値を得ることができました。
(1)…P = -0.11488T2 – 12.0684T + 0.1
(2)…T = {-12.0684 + √(145.6923 – 0.45952P)} / 0.22976
※P/MPa T/℃ (T = -22〜0℃)よって、表2等で記述されている氷の圧力と温度の関係は式(1)及び式(2)より導かれた近似値であり、実測値や理論値ではないことに留意してください。
<水道管凍結のパターン>
図-8:凍結パターン1
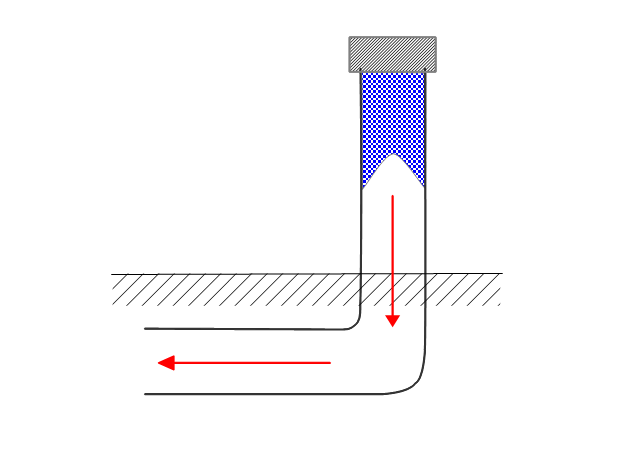
図-8は水道管の末端部から凍結した場合の模式図です。この場合、凍結による圧力は全て本管へ向かう事になり、凍結破損を起すことはまずあり得ません。
図-9:凍結パターン2
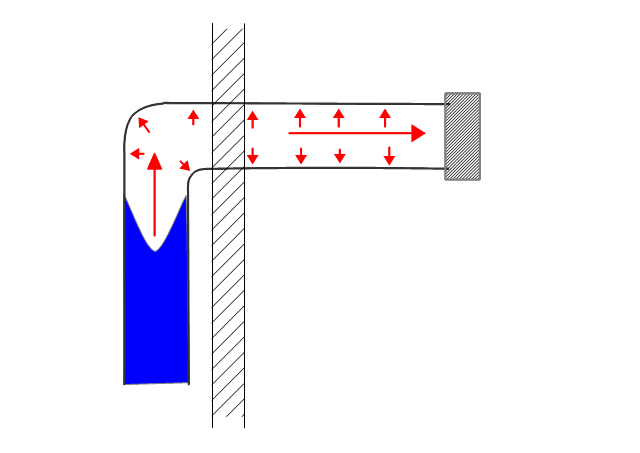
図-9は本管側から凍結が起こった場合の模式図です。氷の成長に伴い圧力を受ける面積は少なくなっていく為、最終的に末端部に近いほど圧力を受けやすくなることを意味します。なお、エルボにかかる圧力は、水道管を動かす力となります。
図-10:凍結パターン3
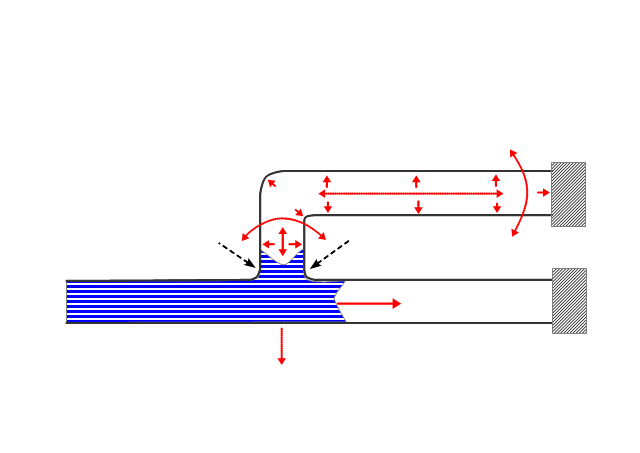
図-10はT字管で凍結が起きた場合の模式図です。今までは単純に内側からの圧力について考察して来ましたが、図-10のような配管で凍結が起きると、別の力が作用してきます。
凍結で水道管が膨張するということは、水道管が変形を起すということですが、これは同時に水道管がごく僅かでも動くことを意味します。
(※5の実験においても鋼管の伸縮が確認されています)
図-10のようにT字管で凍結が起きた場合、下の管は接続部で下向きの力を受けます。
また、上に接続された管はエルボで力の向きが変更されることにより、弧矢印のように管そのものが力を受けます。配管の固定具合により変わってきますが、図-10ではこれら管を動かす力は全て黒破線矢印が示す部分に集中することになります。
例えとしてはあまり良くないのですが、割り箸の両端を手に持ち力を加えた場合を考えてみると、力いっぱいに引っ張っても千切れることはまずありませんが、曲げる力を加えると簡単に折ることができます。この時、割り箸が作る弧の内側では圧縮応力が、外側では引張応力が働き、せん断応力によって破壊されることになります。
図-10の黒破線矢印の部分では元々内側からせん断応力が働いているところに、更に水道管の動きが加わることで応力が集中し、本来であれば水道管の凍結破損を引き起こさない温度であっても合成された応力が水道管の強度を超えてひずみが増加し、水道管の破壊が起こり得ることを示唆しています。
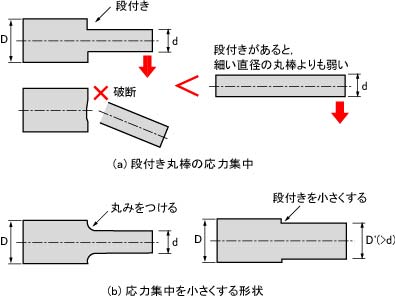
図-11は応力の集中についてのものです。同一の長さ、同一の材質で出来た丸棒において一端を固定し、残りの一端に荷重を加えると、図のように均一の直径のものの方が、段付きで途中から太くなるものより強度が強いことを示しています。これは直径が均一のものは応力が分散されるのに対し、段付きのものはそこに応力が集中するためです。
実際に凍結破損を起こした水道管を見てみると、その多くが末端部やエルボ、T字管付近など、応力が集中しやすい箇所で破損している事が分かります。
水を静かに冷やして行くと-4℃まで凍らないことがあるのですが、この現象は過冷却と呼ばれています。凍結による圧力の発生を調べた実験で、-5℃付近から急激に圧力が上昇しているのもこの過冷却が原因であると推定されています。
以上の点をまとめると、- 4℃ 以下の温度では水道管が凍結する恐れがあり、凍結が起きるのなら水道管の凍結破損が起きたとしても何ら不思議ではない、と結論できます。
凍結破損のメカニズムについては以上です。
次回からはK技研が行った実験に対する反論へと移ります。
<<凍結破損裁判(その6)へ続く>>
最終更新日:2015/03/04(水) 09:15:12
Posted by マスター

posted by マスター
posted by じゅんじゅん
posted by マスター
posted by じゅんじゅん
posted by jp3brx